【考察】気になる! ドライブトレイン全体の駆動効率

力の限りペダルを漕いでいると僅かなパワーロスも見逃せませんよね。
どうすればパワーロスを抑える事ができるか知りたい人。
ドライブトレイン全体の駆動効率を知りたい人
ドライブトレイン全体の駆動効率が気になる人
ドライブトレイン全体の駆動効率についてまとめました。
この記事を読んで、駆動効率を上げて速く走りましょう。
それでは、どうぞ。
目次
本記事の要約
スプロケットの歯数が多くなる程、駆動効率が高くなります。
チェーンテンションが高くなる程、駆動効率が高くなります。
チェーン速度が遅くなる程、駆動効率が高くなります。
チェーンラインのズレは駆動効率に大きく影響しません。
駆動効率を検証した論文

出典:Effects of Frictional Loss on Bicycle Chain Drive Efficiency
自転車のドライブトレインの駆動効率について検証している論文があります。
論文のタイトルは「Effects of Frictional Loss on Bicycle Chain Drive Efficiency」です。
この論文には、駆動効率に大きく影響を与えている要素はチェーンテンションとスプロケットの歯数であると冒頭に書かれています。
この論文は駆動効率の計算式と駆動効率を実測した時のデータの2部構成になっています。
論文に掲載されているデータは以下の通りです。
表1 15Tのみチェーンラインを真っ直ぐにしてテストした
※ケイデンスとパワーの並び方は違うので注意
ケイデンス 50 60 70 60 60 パワー 100w 100w 100w 150w 175w 11T 92.5% 91.1% 88.7% 94.6% 95.5% 15T 94.7% 92.3% 90.4% 96.2% 97.5% 21T 95.2% 93.8% 92.0% 97.4% 98.2% 表2 出力を固定し、ケイデンスを変化させた
ケイデンス 30 40 50 60 70 80 90 パワー 100w 100w 100w 100w 100w 100w 100w 11T 96.7% 95.0% 92.8% 90.9% 89.3% 87.5% 85.4% 15T 97.8% 96.5% 94.6% 93.0% 91.0% 89.3% 87.2% 21T — 97.8% 95.9% 94.4% 92.8% 91.3% 89.8% 表3 ケイデンスを固定し、出力を変化させた
ケイデンス 60 60 60 60 60 60 60 パワー 50w 75w 100w 125% 150w 175w 200w 11T 81.0% 87.4% 91.0% 93.0% 94.4% 95.3% 95.8% 15T 83.2% 89.8% 93.2% 95.1% 96.5% 97.5% 98.0% 21T 85.5% 91.1% 94.4% 96.0% 97.2% 98.1% 98.6% 出典:Effects of Frictional Loss on Bicycle Chain Drive Efficiency
歯数が多くなる程効率が良い
フロントチェーンリング52T、入力パワー100w、60ケイデンス、チェーンライン真っ直ぐの条件でリアスプロケットを11Tと15Tと21Tをそれぞれ計測した所、以下の結果になりました。
52-11 効率91.4%
効率差分 1.8%
52-15 効率93.2%
効率差分 1.8%
52-21 効率95.0%
このことから、リアスプロケットの歯数が多くなる程駆動効率が上がる事が分かります。
歯数が多くなる程スプロケットからチェーンが嚙み合ったり離れたりする時の振れが小さくなりますので、チェーンが振動しづらくパワーロスが軽減できます。
チェーンテンションが高い程効率が良い
チェーンテンションが高い程駆動効率が良いです。
表3を見てみます。
表3 ケイデンスを固定し、出力を変化させた
| ケイデンス | 60 | 60 | 60 | 60 | 60 | 60 | 60 |
| パワー | 50w | 75w | 100w | 125% | 150w | 175w | 200w |
| 11T | 81.0% | 87.4% | 91.0% | 93.0% | 94.4% | 95.3% | 95.8% |
| 15T | 83.2% | 89.8% | 93.2% | 95.1% | 96.5% | 97.5% | 98.0% |
| 21T | 85.5% | 91.1% | 94.4% | 96.0% | 97.2% | 98.1% | 98.6% |
この表は同じケイデンスでパワーのみ変化させています。
実走では勾配の違う道を同じケイデンスで走った場合に相当します。
ケイデンスが同じでパワーを上げていきますと、チェーンテンションがパワーに比例して高くなる事になります。
15Tで見てみますとパワー50wの時の駆動効率データは83.2%に対して、パワー200wの時の駆動効率データは98.0%まで向上しました。
そして、チェーンテンションによる影響はリアスプロケットの歯数による影響より大きいです。
表2を見てみます。
表2 出力を固定し、ケイデンスを変化させた
| ケイデンス | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| パワー | 100w | 100w | 100w | 100w | 100w | 100w | 100w |
| 11T | 96.7% | 95.0% | 92.8% | 90.9% | 89.3% | 87.5% | 85.4% |
| 15T | 97.8% | 96.5% | 94.6% | 93.0% | 91.0% | 89.3% | 87.2% |
| 21T | — | 97.8% | 95.9% | 94.4% | 92.8% | 91.3% | 89.8% |
表の黄色と緑色はそれぞれほぼ同じ速度です。
ケイデンスを変えて同じ速度になる様にして走った場合、スプロケットの歯数は小さい方が駆動効率は高くなる事が表のデータから分かります。
チェーン速度が遅い程効率が良い
同じ11Tとチェーン張力でも、チェーンリングが小さいと駆動効率が良い傾向です。
表2のパワー100w 30ケイデンスと表3のパワー200w 60ケイデンスで比較します。
表2のパワー100w 30ケイデンスのデータでケイデンスを2倍にしますと60ケイデンスになります。
その場合、パワーも2倍になりますので200wになります。
ただしパワーをケイデンスで稼いでいますので、チェーンテンションは変わらずチェーン速度のみ2倍になります。
下記表は表2と表3の実データを組み合わせたものです。
| 表2 | 表3 | |
| ケイデンス | 30 | 60 |
| チェーン速度 | 0.33m/s | 0.66m/s |
| パワー | 100w | 200w |
| 11T | 96.7% | 95.8% |
| 15T | 97.8% | 98.0% |
| 21T | — | 98.6% |
21Tのデータは欠落していますので比較できません。
15Tの場合はチェーン速度が変わっていても駆動効率はほぼ同じですが、11Tの場合ではチェーン速度が遅い方は駆動効率が0.9%高い結果になっています。
チェーンラインのズレによる影響は小さい
チェーンラインのズレによる影響は小さいです。
論文で実測されたリアスプロケット11T パワー100w 60ケイデンスのデータを見てみます。
| チェーンライン | 効率 |
| 真っ直ぐ | 91.4% |
| ズレ有(表1) | 91.1% |
このデータから計測器の誤差0.2%を加えますと最大で0.5%の駆動効率がチェーンラインの状態によっては変わります。
ですが、スプロケットの歯数やチェーンテンションによる影響よりも小さく限定的ですので、アウターローやインナートップの組み合わせになったとしても、体感できる程の駆動効率の違いが分からない事になります。
ドライブトレイン効率計算フォーム
当ブログで公開した計算式を計算フォームにしました。
11Tから21Tまでで50wから200wまでの再現性は実測値と比較していますのでほぼ正確に算出できますが、その範囲を超えて計算しますと実測値がなく検証できない為、実際の効率と差が出る可能性がありますのでご了承下さい。
駆動効率の計算式を作る
論文には駆動損失の計算式が掲載されていますが、実際に計算した所実測値を計算結果から再現する事ができませんでした。
そこで、論文の表2と表3のデータを用いて計算フォームを作りました。
計算フォームを作る上で、その過程を公開します。
効率から逆算して係数を求める
まずは表3のデータを用いて計算式を考えます。
表3ではケイデンスは変えずにパワーとリアスプロケットを変えた時の駆動効率が掲載されています。
駆動効率はこの記事では下記計算式で考えました。
※この記事では、チェーンテンションの単位”N”はSI単位の「ニュートン」を用いています。
\(駆動効率=1-\frac{係数}{チェーンテンション(N)}\)
表3で分かっている情報はチェーンリングとスプロケットの歯数とパワーとケイデンスです。
まずは、チェーンリングの歯数とパワーとケイデンスの情報を用いてチェーンテンションを計算します。
チェーンテンションは下記計算式で求められます。
\(チェーンテンション(N)=\frac{パワー(w)\times60(秒)}{ケイデンス\times2\times3.14(円周率\pi)\timesチェーンリング半径(m)}\)
チェーンテンションを求める事ができましたら、チェーンテンションと駆動効率の実データを用いて係数を計算します。
実データから駆動効率については分かっていますが係数が分かりませんので、駆動効率の計算式を組み替えて係数を求められる計算式にしました。
\(係数=チェーンテンション(N)-(駆動効率\timesチェーンテンション(N))\)
この係数を求められる計算式を用いて下記表を埋めていきます。
| 歯数 | 50w | 75w | 100w | 125w | 150w | 175w | 200w |
| 11T | |||||||
| 15T | |||||||
| 21T |
表を埋めますと下記表の様になりました。
| 歯数 | 50w | 75w | 100w | 125w | 150w | 175w | 200w |
| 11T | 14.383 | 14.301 | 13.617 | 13.244 | 12.712 | 12.446 | 12.713 |
| 15T | 12.718 | 11.577 | 10.288 | 9.271 | 7.945 | 6.620 | 6.054 |
| 21T | 10.977 | 10.102 | 8.473 | 7.568 | 6.356 | 5.031 | 4.238 |
各スプロケット別の係数を求める
上記表を用いて各スプロケット別の係数を求めます。
上記表より11Tの係数を抜粋
| 歯数 | 50w | 75w | 100w | 125w | 150w | 175w | 200w |
| 11T | 14.383 | 14.301 | 13.617 | 13.244 | 12.712 | 12.446 | 12.713 |
まずは11Tのスプロケットの係数グラフを作成します。
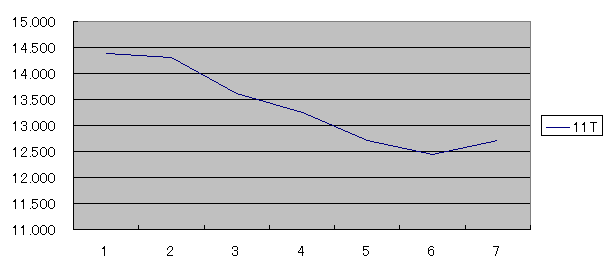
200wのデータが175wより大きくなっている為、グラフの最後が上に向いています。
この場合は175wまでのグラフになる様にデータ範囲を狭めます。
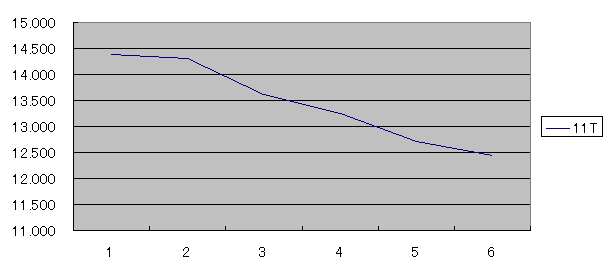
このグラフを見る限りでは直線に右肩下がりのグラフになっています。
そこで近似曲線の計算式を表示させます。
折れ線グラフを右クリックして近似曲線の追加を選択します。
そして、線形近似を選択します。
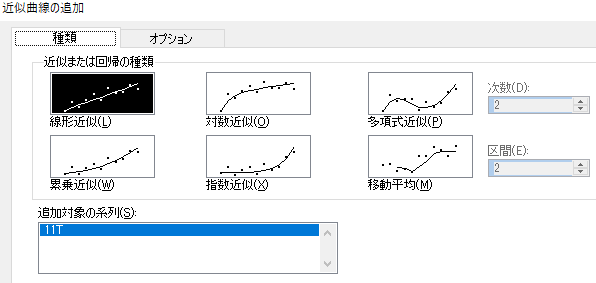
次にオプションタブの「グラフに数式を表示する」にチェックを入れます。
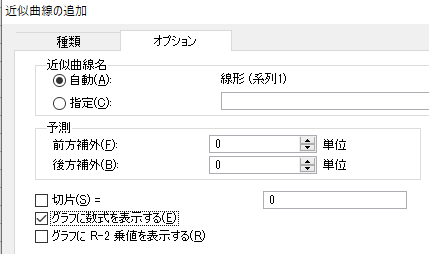
そうする事でグラフに近似曲線と近似曲線の計算式が表示されます。
表示させた11Tの計算式は下記になります。
\(y=14.933-(0.4236\times7)=11.967\)
表示させた計算式を用いて、200wの係数を求めますと11.967になりました。
15Tと21Tは200wの係数がそのまま使えますので、係数は下記表の値になりました。
| 50w | 200w | |
| 11T | 14.383 | 11.967 |
| 15T | 12.718 | 6.054 |
| 21T | 10.976 | 4.238 |
50wと200wの60Tまでの係数を求める
「各スプロケット別の係数を求める」で作った表の係数を用いて、31T 41T 51T 61T の係数を求めます。
まずは、計算された係数を用いて、31T 41T 51T 61T の係数を求める為の累乗係数を下記計算式から計算します。
\(累乗係数=\frac{\log(21Tの係数)}{\log(11Tの係数)}\)
計算した所、累乗係数は 0.898 になりました。
次に、計算した累乗係数を用いて 31T の係数を下記計算式から求めます。
\(31Tの係数=21Tの係数^{0.898}\)
41T 51T 61T の係数も同じ要領で41T から順番に求めていきます。
計算した所、係数は下記表の値になりました。
| 50w | 200w | |
| 11T | 14.383 | 11.967 |
| 15T | 12.718 | 6.054 |
| 21T | 10.976 | 4.238 |
| 31T | 8.610 | 2.317 |
| 41T | 6.921 | 1.630 |
| 51T | 5.689 | 1.329 |
| 61T | 4.769 | 1.180 |
各パワー別の係数を求める
「各スプロケット別の係数を求める」で計算した係数を用いて、各パワー別の係数を求めます。
50wと200wの係数は計算済みですので、150w間隔でチェーンが切れるチェーンテンションになるまで係数を計算します。
チェーンテンションは下記計算式で求められます。
\(チェーンテンション(N)=\frac{パワー(w)\times60(秒)}{ケイデンス\times2\times3.14(円周率\pi)\timesチェーンリング半径(m)}\)
チェーンテンションの限界値は下記ブログから引用した所、3,630Nまで許容できます。
ですので、52Tのチェーンリングでチェーンにパワーを伝達した場合、150wずつパワーを上げていきますと2,450wぐらいでチェーンテンションの限界値に到達します。
各パワー別の係数の求め方は「50wと200wの60Tまでの係数を求める」と同じ要領です。
累乗係数を求めた後、各パワー別の係数を下記計算式から求めます。
\(スプロケット累乗係数=\frac{\log(200wの係数)}{\log(50wの係数)}\)
\(350wの係数=200wの係数^{スプロケット累乗係数}\)
\(500wの係数=350wの係数^{スプロケット累乗係数}\)
計算した所、係数は下記表の値になりました。
| 350w | 500w | 650w | …… | …… | 2,150w | 2,300w | 2,450w | |
| 11T | 10.085 | 8.600 | 7.414 | …… | …… | 2.666 | 2.492 | 2.340 |
| 15T | 3.579 | 2.467 | 1.895 | …… | …… | 1.020 | 1.014 | 1.010 |
| 21T | 2.388 | 1.690 | 1.372 | …… | …… | 1.002 | 1.001 | 1.001 |
| 31T | 1.388 | 1.136 | 1.051 | …… | …… | 1.000 | 1.000 | 1.000 |
| 41T | 1.131 | 1.032 | 1.008 | …… | …… | 1.000 | 1.000 | 1.000 |
| 51T | 1.048 | 1.008 | 1.001 | …… | …… | 1.000 | 1.000 | 1.000 |
| 61T | 1.018 | 1.002 | 1.000 | …… | …… | 1.000 | 1.000 | 1.000 |
その後、11T 15T 21T 31T 41T 51T 61T の中間ギヤの係数を按分して中間値を入れていきます。
中間値を入れた所、下記表の値になりました。
| 50w | 200w | 350w | 500w | 650w | …… | …… | 2,450w | |
| 11T | 14.383 | 11.968 | 10.085 | 8.600 | 7.414 | …… | …… | 2.340 |
| 12T | 13.967 | 10.489 | 8.459 | 7.066 | 6.034 | …… | …… | 2.007 |
| 13T | 13.550 | 9.011 | 6.832 | 5.533 | 4.655 | …… | …… | 1.675 |
| 14T | 13.134 | 7.532 | 5.206 | 4.000 | 3.275 | …… | …… | 1.343 |
| 15T | 12.718 | 6.054 | 3.579 | 2.467 | 1.895 | …… | …… | 1.010 |
| 16T | 12.427 | 5.751 | 3.381 | 2.337 | 1.808 | …… | …… | 1.009 |
| 17T | 12.137 | 5.449 | 3.182 | 2.208 | 1.721 | …… | …… | 1.007 |
| 18T | 11.847 | 5.146 | 2.983 | 2.078 | 1.634 | …… | …… | 1.005 |
| 19T | 11.557 | 4.843 | 2.785 | 1.949 | 1.546 | …… | …… | 1.004 |
| 20T | 11.267 | 4.541 | 2.586 | 1.819 | 1.459 | …… | …… | 1.002 |
| 21T | 10.977 | 4.238 | 2.388 | 1.690 | 1.372 | …… | …… | 1.001 |
| … | …… | …… | …… | …… | …… | …… | …… | …… |
| … | …… | …… | …… | …… | …… | …… | …… | …… |
| 61T | 4.769 | 1.180 | 1.018 | 1.002 | 1.000 | …… | …… | 1.000 |
係数を駆動効率に変換する
ここまでの過程で求めた係数を駆動効率に変換します。
駆動効率は下記計算式から求められます。
\(駆動効率=1-\frac{係数}{チェーンテンション(N)}\)
係数を駆動効率に変換した所、下記表の値になりました。
| 50w | 200w | 350w | 500w | 650w | …… | …… | 2,450w | |
| 11T | 0.810 | 0.960 | 0.981 | 0.989 | 0.992 | …… | …… | 0.999 |
| 12T | 0.816 | 0.965 | 0.984 | 0.991 | 0.994 | …… | …… | 0.999 |
| 13T | 0.821 | 0.970 | 0.987 | 0.993 | 0.995 | …… | …… | 1.000 |
| 14T | 0.827 | 0.975 | 0.990 | 0.995 | 0.997 | …… | …… | 1.000 |
| 15T | 0.832 | 0.980 | 0.993 | 0.997 | 0.998 | …… | …… | 1.000 |
| 16T | 0.836 | 0.981 | 0.994 | 0.997 | 0.998 | …… | …… | 1.000 |
| 17T | 0.840 | 0.982 | 0.994 | 0.997 | 0.998 | …… | …… | 1.000 |
| 18T | 0.844 | 0.983 | 0.994 | 0.997 | 0.998 | …… | …… | 1.000 |
| 19T | 0.847 | 0.984 | 0.995 | 0.997 | 0.998 | …… | …… | 1.000 |
| 20T | 0.851 | 0.985 | 0.995 | 0.998 | 0.999 | …… | …… | 1.000 |
| 21T | 0.855 | 0.986 | 0.995 | 0.998 | 0.999 | …… | …… | 1.000 |
| … | …… | …… | …… | …… | …… | …… | …… | …… |
| … | …… | …… | …… | …… | …… | …… | …… | …… |
| 61T | 0.936 | 0.996 | 0.998 | 0.999 | 0.999 | …… | …… | 1.000 |
チェーンリング52Tのみの駆動効率を求める
52T片側のみの駆動効率を求めます。
駆動効率はフロントチェーンリングからチェーンでリアスプロケットにパワーを伝達してハブを回した時、チェーンリングに伝えた力がどの程度までハブに伝えられたかを表した値です。
そして、フロントチェーンリングとリアスプロケットの乗算値が駆動効率になります。
ですので、片側のみの駆動効率とする場合は両側の効率の平方根を求めればいいです。
計算式で表しますと下記になります。
\(フロント52Tの駆動効率=\sqrt{フロント52Tとリア52Tの駆動効率}\)
計算した所、チェーンリング52Tは下記表の駆動効率になりました。
| 50w | 200w | 350w | 500w | 650w | …… | …… | 2,450w |
| 0.962 | 0.998 | 0.999 | 0.999 | 0.999 | …… | …… | 1.000 |
フロントの駆動効率を除算する
「チェーンリング52Tのみの駆動効率を求める」でチェーンリング52Tの駆動効率を求めましたので、各パワーとスプロケット別の駆動効率をフロントの駆動効率で除算します。
\(リアのみの駆動効率=\frac{全体の駆動効率}{フロントの駆動効率}\)
各駆動効率をフロントの駆動効率で除算した所、下記表の値になりました。
| 50w | 200w | 350w | 500w | 650w | …… | …… | 2,450w | |
| 11T | 0.842 | 0.963 | 0.982 | 0.989 | 0.993 | …… | …… | 1.000 |
| 12T | 0.847 | 0.967 | 0.985 | 0.991 | 0.994 | …… | …… | 1.000 |
| 13T | 0.853 | 0.972 | 0.988 | 0.993 | 0.996 | …… | …… | 1.000 |
| 14T | 0.859 | 0.977 | 0.991 | 0.995 | 0.997 | …… | …… | 1.000 |
| 15T | 0.865 | 0.982 | 0.994 | 0.997 | 0.999 | …… | …… | 1.000 |
| 16T | 0.869 | 0.983 | 0.995 | 0.998 | 0.999 | …… | …… | 1.000 |
| 17T | 0.873 | 0.984 | 0.995 | 0.998 | 0.999 | …… | …… | 1.000 |
| 18T | 0.877 | 0.985 | 0.995 | 0.998 | 0.999 | …… | …… | 1.000 |
| 19T | 0.881 | 0.986 | 0.996 | 0.998 | 0.999 | …… | …… | 1.000 |
| 20T | 0.884 | 0.987 | 0.996 | 0.998 | 0.999 | …… | …… | 1.000 |
| 21T | 0.888 | 0.988 | 0.996 | 0.998 | 0.999 | …… | …… | 1.000 |
| … | …… | …… | …… | …… | …… | …… | …… | …… |
| … | …… | …… | …… | …… | …… | …… | …… | …… |
| 60T | 0.972 | 0.998 | 0.999 | 0.999 | 0.999 | …… | …… | 1.000 |
片側のみの駆動効率を係数に再変換する
「フロントの駆動効率を除算する」で計算した片側のみの駆動効率を係数に再変換します。
計算式は下記になります。
\(係数=チェーンテンション(N)-(駆動効率\timesチェーンテンション(N))\)
上記計算式で計算した所、下記表の係数になりました。
| 50w | 200w | 350w | 500w | 650w | …… | …… | 2,450w | |
| 11T | 11.982 | 11.335 | 9.572 | 8.101 | 6.917 | …… | …… | 1.840 |
| 12T | 11.550 | 9.853 | 7.944 | 6.567 | 5.536 | …… | …… | 1.507 |
| 13T | 11.117 | 8.371 | 6.316 | 5.033 | 4.156 | …… | …… | 1.175 |
| 14T | 10.684 | 6.890 | 4.688 | 3.499 | 2.776 | …… | …… | 0.843 |
| 15T | 10.252 | 5.408 | 3.060 | 1.964 | 1.395 | …… | …… | 0.510 |
| 16T | 9.950 | 5.105 | 2.861 | 1.835 | 1.308 | …… | …… | 0.509 |
| 17T | 9.649 | 4.801 | 2.662 | 1.705 | 1.221 | …… | …… | 0.507 |
| 18T | 9.347 | 4.498 | 2.463 | 1.576 | 1.133 | …… | …… | 0.506 |
| 19T | 9.046 | 4.195 | 2.265 | 1.446 | 1.046 | …… | …… | 0.504 |
| 20T | 8.744 | 3.891 | 2.066 | 1.317 | 0.959 | …… | …… | 0.502 |
| 21T | 8.443 | 3.588 | 1.867 | 1.187 | 0.872 | …… | …… | 0.501 |
| … | …… | …… | …… | …… | …… | …… | …… | …… |
| … | …… | …… | …… | …… | …… | …… | …… | …… |
| 60T | 2.088 | 0.538 | 0.499 | 0.499 | 0.500 | …… | …… | 0.500 |
チェーンテンションから係数を計算できる様にする
「片側のみの駆動効率を係数に再変換する」で計算した係数から中間値を求める事で、チェーンテンションから係数を求める事ができます。
初期値となる係数を求める
まずは初期値となる係数を求めます。
計算式は下記になります。
\(係数初期値=テンション始点\times\frac{係数始点-係数終点}{テンション終点-テンション始点}+係数始点\)
例えば下記チェーンテンションと係数の場合、この様に計算式に代入して計算します。
| パワー | 50w | 200w |
| テンション | 75.7N | 302.7N |
| 係数 | 11.982 | 11.335 |
\(係数初期値=75.7(N)\times\frac{11.982-11.335}{302.7(N)-75.7(N)}+11.982=12.198\)
上記計算式で計算した所、下記表の係数になりました。
| 50w | — | 200w | — | 350w | — | |
| 75.7N | — | 302.7N | — | 529.7N | — | |
| 11T | — | 0.003 | — | 0.008 | — | 0.006 |
| 12T | — | 0.007 | — | 0.008 | — | 0.006 |
| 13T | — | 0.012 | — | 0.009 | — | 0.006 |
| 14T | — | 0.017 | — | 0.01 | — | 0.005 |
| 15T | — | 0.021 | — | 0.01 | — | 0.005 |
| 16T | — | 0.021 | — | 0.01 | — | 0.005 |
| 17T | — | 0.021 | — | 0.009 | — | 0.004 |
| 18T | — | 0.021 | — | 0.009 | — | 0.004 |
| 19T | — | 0.021 | — | 0.009 | — | 0.004 |
| 20T | — | 0.021 | — | 0.008 | — | 0.003 |
| 21T | — | 0.021 | — | 0.008 | — | 0.003 |
| … | — | …… | — | …… | — | …… |
| … | — | …… | — | …… | — | …… |
| 60T | — | 0.007 | — | 0 | — | 0 |
係数の変動値を求める
次に係数の変動値を求めます。
計算式は下記になります。
\(係数変動値=\frac{係数始点-係数終点}{テンション終点-テンション始点}\)
上記計算式で計算した所、下記表の係数になりました。
| 50w | — | 200w | — | 350w | — | |
| 75.7N | — | 302.7N | — | 529.7N | — | |
| 11T | — | 0.003 | — | 0.008 | — | 0.006 |
| 12T | — | 0.007 | — | 0.008 | — | 0.006 |
| 13T | — | 0.012 | — | 0.009 | — | 0.006 |
| 14T | — | 0.017 | — | 0.01 | — | 0.005 |
| 15T | — | 0.021 | — | 0.01 | — | 0.005 |
| 16T | — | 0.021 | — | 0.01 | — | 0.005 |
| 17T | — | 0.021 | — | 0.009 | — | 0.004 |
| 18T | — | 0.021 | — | 0.009 | — | 0.004 |
| 19T | — | 0.021 | — | 0.009 | — | 0.004 |
| 20T | — | 0.021 | — | 0.008 | — | 0.003 |
| 21T | — | 0.021 | — | 0.008 | — | 0.003 |
| … | — | …… | — | …… | — | …… |
| … | — | …… | — | …… | — | …… |
| 60T | — | 0.007 | — | 0 | — | 0 |
チェーンテンションを代入して係数を求める
フロント52T、リア11Tを使用して200w 60ケイデンスでペダルを漕いでいる場合、歯数52Tと11Tの係数始点と係数変動値を使用します。
52Tのチェーンリングを200w 60ケイデンスで回した場合、チェーンテンションは302.7Nになります。
次にフロントとリアの係数を下記計算式から求めます。
\(係数=係数初期値-(変動係数\timesチェーンテンション(N))\)
フロント52T
\(52Tの係数=0.838-(0.000596\times302.7(N))=0.657\)
リア11T
\(11Tの係数=13.685-(0.007765\times302.7(N))=11.333\)
計算した結果、52Tの係数は0.657、11Tの係数は11.333になりました。
フロントとリアの駆動効率を求める
200w 60ケイデンスで52Tのチェーンリングと11Tのスプロケットを回した時のフロントとリアの駆動効率を求めます。
計算式は下記になります。
\(駆動効率=1-\frac{係数}{チェーンテンション(N)}\)
「チェーンテンションを代入して係数を求める」で計算した係数を代入して駆動効率を計算した所、フロントは0.998 リアは0.963 になりました。
ドライブトレイン全体の駆動効率を求める
ペダルに伝えたパワーはフロントのチェーンリングを介してチェーンを経由してリアスプロケットに伝達されます。
ですので、チェーンリング部でパワーロスされた後、スプロケットでさらにパワーロスされます。
そのパワーロスを計算式で表しますと、「フロントチェーンリングの効率×リアスプロケットの効率=ドライブトレイン全体の効率」になります。
「フロントとリアの駆動効率を求める」で求めた駆動効率はフロント0.998 リア0.963でしたので、フロントとリアの駆動効率を乗算しますとドライブトレイン全体の駆動効率は「0.998×0.963=0.960」になりました。
パーセントで表しますと100を乗算すればいいですので、「0.960×100=96.0%」になりました。
チェーン速度を織り込む
ここまでで作成した計算式で駆動効率を計算した所、下記表の値になりました。
表3 ケイデンスを固定し、出力を変化させた
| パワー | 50w | 75w | 100w | 125w | 150w | 175w | 200w |
11T
| 実測値 | 81.0% | 87.4% | 91.0% | 93.0% | 94.4% | 95.3% | 95.8% |
| 計算値 | 81.0% | 87.6% | 90.9% | 93.0% | 94.3% | 95.3% | 96.0% |
15T
| 実測値 | 83.2% | 89.8% | 93.2% | 95.1% | 96.5% | 97.5% | 98.0% |
| 計算値 | 83.5% | 89.7% | 93.0% | 95.0% | 96.3% | 97.3% | 98.0% |
21T
| 実測値 | 85.5% | 91.1% | 94.4% | 96.0% | 97.2% | 98.1% | 98.6% |
| 計算値 | 85.5% | 91.2% | 94.2% | 95.9% | 97.1% | 98.0% | 98.6% |
表3では実測値とほぼ同じ効率を再現できました。
では、表2でも比較してみます。
表2 出力を固定し、ケイデンスを変化させた
| ケイデンス | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
11T
| 実測値 | 96.7% | 95.0% | 92.8% | 90.9% | 89.3% | 87.5% | 85.4% |
| 計算値 | 96.0% | 94.3% | 92.6% | 90.9% | 89.3% | 87.6% | 85.9% |
15T
| 実測値 | 97.8% | 96.5% | 94.6% | 93.0% | 91.0% | 89.3% | 87.2% |
| 計算値 | 98.0% | 96.3% | 94.6% | 93.0% | 91.3% | 89.7% | 88.0% |
21T
| 実測値 | - | 97.8% | 95.9% | 94.4% | 92.8% | 91.3% | 89.8% |
| 計算値 | - | 97.1% | 95.6% | 94.2% | 92.7% | 91.2% | 89.8% |
表2では計算値が実測値と若干ズレています。
グラフで表しますとこの様になります。
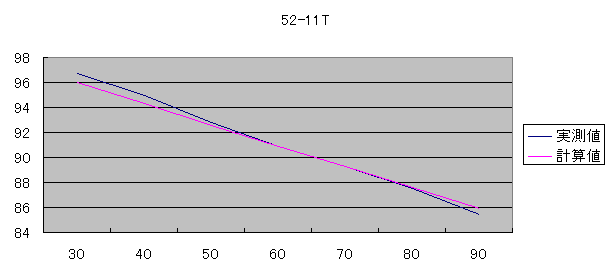
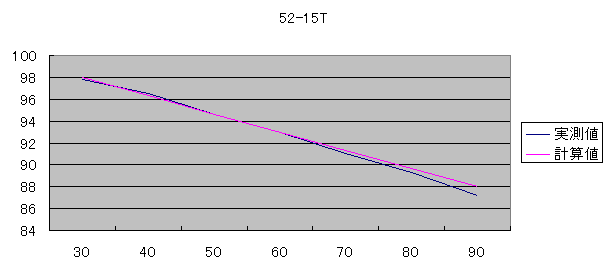
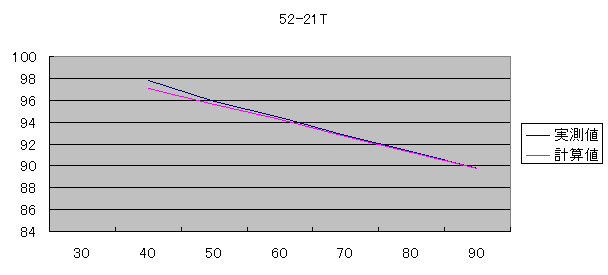
駆動効率のズレ幅を修正する
表2では計算値が実測値と若干ズレています。
ズレ幅は以下の通りです。
| ケイデンス | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| 11T | 0.7 | 0.7 | 0.2 | 0 | 0 | -0.1 | -0.5 |
| 15T | -0.2 | 0.2 | 0 | 0 | -0.3 | -0.4 | -0.8 |
| 21T | 0.7 | 0.3 | 0.2 | 0.1 | 0.1 | 0 |
補正前の駆動効率はチェーンテンションを織り込んだ値ですので、ペダルに伝えたパワーから補正前の駆動効率を減算した値の範囲内で駆動効率を修正します。
そのスレ幅を修正する補正値は下記計算式から計算できます。
\(補正値=\frac{補正後の駆動効率}{補正前の駆動効率}-1\)
各項目でズレ幅が一番小さくなる様に補正値を算出した所、補正値は0.003027になりました。
駆動効率に補正値を加える
フロント52T リア11T を90ケイデンスで回した場合の補正前駆動効率は0.935で、チェーン速度は59.472m/minになります。
「駆動効率のズレ幅を修正する」でフロント52Tリア11Tの補正値を求めた所、補正値は0.003027でした。
補正前のズレ幅は60ケイデンスが一番ズレ幅が小さかったですので、60ケイデンスを基準チェーン速度39.648m/minとします。
この値を下記計算式に代入して計算します。
\(補正後の駆動効率=\)
\((1-補正前の駆動効率)\times((基準チェーン速度-チェーン速度)\times0.003027)+補正前の駆動効率\)
\(=(1-0.935)\times((39.648-59.472)\times0.003027)+0.935\)
\(=0.931\)
チェーン速度補正後のドライブトレイン全体の駆動効率は0.931になりました。
パーセントで表しますと100を乗算すればいいですので、「0.931×100=93.1%」になりました。
計算式の再現性を検証
計算過程を長文で説明しましたが、計算式の再現性を検証します。
比較元の実測値と、参考としてcbnblog(CBN)で公開されているチェーン駆動効率の計算式から得られたデータと比較します。
表3 ケイデンスを固定し、出力を変化させた
| パワー | 50w | 75w | 100w | 125w | 150w | 175w | 200w |
11T
| 実測値 | 81.0% | 87.4% | 91.0% | 93.0% | 94.4% | 95.3% | 95.8% |
| 計算値 | 81.0% | 87.6% | 90.9% | 93.0% | 94.3% | 95.3% | 96.0% |
| CBN | 78.7% | 87.4% | 91.3% | 93.5% | 94.8% | 95.8% | 96.4% |
15T
| 実測値 | 83.2% | 89.8% | 93.2% | 95.1% | 96.5% | 97.5% | 98.0% |
| 計算値 | 83.2% | 89.7% | 93.0% | 95.0% | 96.3% | 97.3% | 98.0% |
| CBN | 83.4% | 90.2% | 93.2% | 94.9% | 96.0% | 96.7% | 97.2% |
21T
| 実測値 | 85.5% | 91.1% | 94.4% | 96.0% | 97.2% | 98.1% | 98.6% |
| 計算値 | 85.6% | 91.2% | 94.2% | 95.9% | 97.1% | 98.0% | 98.6% |
| CBN | 87.1% | 92.3% | 94.7% | 96.0% | 96.9% | 97.4% | 97.8% |
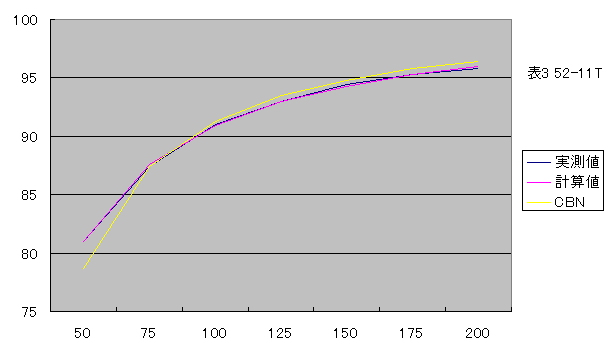
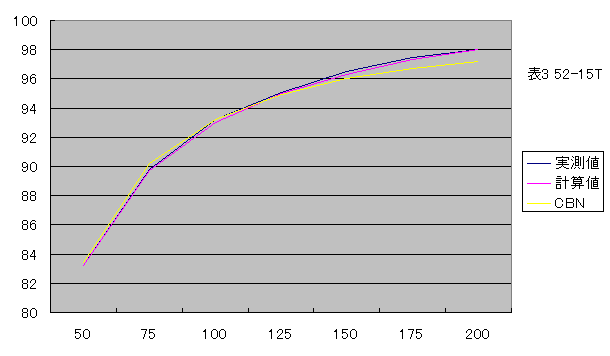
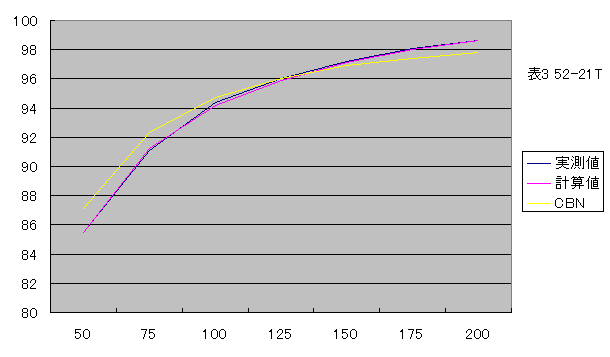
当ブログで得られた計算値とcbnblogで得られた計算値を、実測値との差として比較します。
表3 ケイデンスを固定し、出力を変化させた
| パワー | 50w | 75w | 100w | 125w | 150w | 175w | 200w |
11T
| 計算値 | 0 | 0.2 | 0.1 | 0 | 0.1 | 0 | 0.2 | 合計0.6 |
| CBN | 2.3 | 0 | 0.3 | 0.5 | 0.4 | 0.5 | 0.6 | 合計4.6 |
15T
| 計算値 | 0 | 0.1 | 0.2 | 0.1 | 0.2 | 0.2 | 0 | 合計0.8 |
| CBN | 0.2 | 0.4 | 0 | 0.2 | 0.5 | 0.8 | 0.8 | 合計2.9 |
21T
| 計算値 | 0 | 0.1 | 0.2 | 0.1 | 0.1 | 0.1 | 0 | 合計0.6 |
| CBN | 1.6 | 1.2 | 0.3 | 0 | 0.3 | 0.7 | 0.8 | 合計4.9 |
cbnblogの計算式で得られた計算値の乖離値合計は2.9から4.6までと駆動効率としては無視できない値になりました。
一方、当ブログの計算式で得られた計算値の乖離値合計は0.6から0.8までと駆動効率としては誤差の範囲から外れてしまいますが、ズレは小さく収まりました。
各値で見てみますと誤差の範囲に収まっています。
次に、ケイデンスの影響が出る計算値で比較します。
表2 出力を固定し、ケイデンスを変化させた
| ケイデンス | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
11T
| 実測値 | 96.7% | 95.0% | 92.8% | 90.9% | 89.3% | 87.5% | 85.4% |
| 当ブログ | 96.3% | 94.6% | 92.8% | 90.9% | 89.0% | 87.1% | 85.1% |
| CBN | 96.4% | 94.8% | 93.1% | 91.3% | 89.4% | 87.4% | 85.3% |
15T
| 実測値 | 97.8% | 96.5% | 94.6% | 93.0% | 91.0% | 89.3% | 87.2% |
| 当ブログ | 98.1% | 96.5% | 94.7% | 93.0% | 91.1% | 89.3% | 87.3% |
| CBN | 97.2% | 96.0% | 94.6% | 93.2% | 91.7% | 90.2% | 88.5% |
21T
| 実測値 | - | 97.8% | 95.9% | 94.4% | 92.8% | 91.3% | 89.8% |
| 当ブログ | - | 97.2% | 95.7% | 94.2% | 92.5% | 90.9% | 89.2% |
| CBN | - | 96.9% | 95.8% | 94.7% | 93.6% | 92.3% | 91.1% |
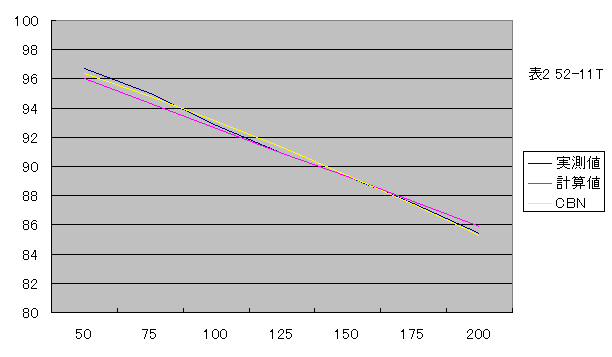
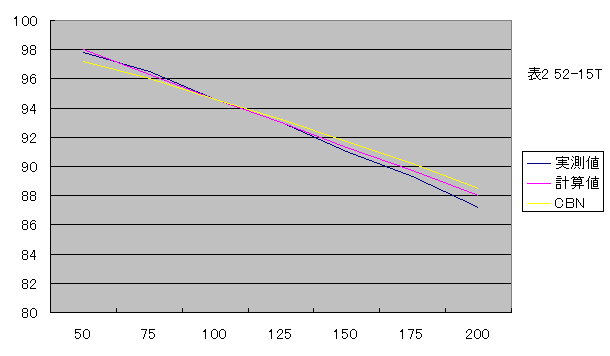
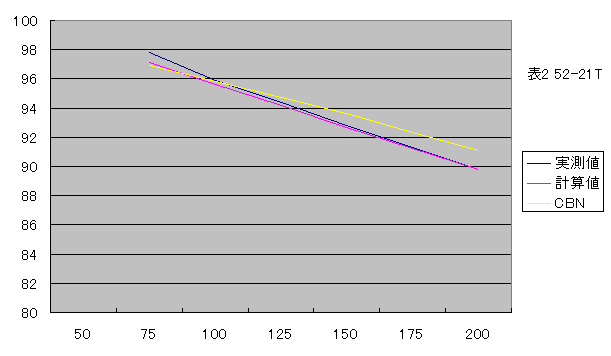
当ブログで得られた計算値とcbnblogで得られた計算値を、実測値との差として比較します。
表2 出力を固定し、ケイデンスを変化させた
| ケイデンス | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
11T
| 当ブログ | 0.4 | 0.4 | 0 | 0 | 0.3 | 0.4 | 0.3 | 合計1.8 |
| CBN | 0.3 | 0.2 | 0.3 | 0.4 | 0.1 | 0.1 | 0.1 | 合計1.5 |
15T
| 当ブログ | 0.3 | 0 | 0.1 | 0 | 0.1 | 0 | 0.1 | 合計0.6 |
| CBN | 0.6 | 0.5 | 0 | 0.2 | 0.7 | 0.9 | 1.3 | 合計4.2 |
21T
| 当ブログ | - | 0.6 | 0.2 | 0.2 | 0.3 | 0.4 | 0.6 | 合計2.3 |
| CBN | - | 0.9 | 0.1 | 0.3 | 0.8 | 1 | 1.3 | 合計4.4 |
cbnblogの計算式で得られた計算値の乖離値合計は1.5から4.4までと駆動効率としては無視できない値になりました。
当ブログの計算式で得られた計算値の乖離値合計は0.6から2.3までと駆動効率としては無視できない値になりましたが、cbnblogの計算値よりズレが小さく収まりました。
各値で見てみますと当ブログの計算値では最大0.6とズレ幅が気になりますが、cbnblogでは最大1.3ですので、ズレ幅はcbnblogの半分に収まっています。
まとめ
スプロケットの歯数が多くなる程、駆動効率が高くなる。
チェーンテンションが高くなる程、駆動効率が高くなる。
チェーン速度が遅くなる程、駆動効率が高くなる。
チェーンラインのズレは駆動効率に大きく影響しない。
脚力に合ったチェーンリングとスプロケットを付けて、効率よく走りましょう。








