エアロスポークは空気抵抗が小さい事は分かりますが、数値化された値までは分からないですよね。
スポークの空気抵抗が分かる。
エアロスポークとラウンドスポークとの空気抵抗の違いについて分かる。
空気抵抗と剛性が両立しているスポーク本数が分かる。
エアロスポークは一般的な丸形状のスポークより空気抵抗がかなり小さいと言われています。
ですが、エアロスポークの効果についてまで分かる情報がありません。
そこで本記事では、スポークの空気抵抗値について取り上げます。
|
【広告】-ここから- 【広告】-ここまで- |
目次
本記事の要約
エアロスポークにするよりもスポーク本数を減らした方が空気抵抗は小さいです。
前輪はエアロスポークを少なめの本数で手組みして、後輪はラウンドスポークを多めの本数で手組みすると良いです。
完組ホイールは剛性が高くて軽いです。
スポークについて

CX-RAYは丸スポークより抵抗が小さい
32本のスポークで組み立てた手組みホイールを用いて3通りのスポークパターンの速度低下値をデータ取りしてから、そのデータを基に空気抵抗値を計算しました。
40km/h走行時のスポーク空気抵抗
| スポーク | 前輪 | 後輪 | |
| CX-RAY | 16本 | 1.78w | 0.60w |
| 2.0-1.8バテッド | 16本 | 2.14w | 0.72w |
| CX-RAY | 32本 | 2.29w | 0.77w |
| 2.0-1.8バテッド | 32本 | 2.76w | 0.92w |
前輪の空気抵抗計算値を見てみますと、スポーク本数16本の時でCX-RAYは2.0-1.8バテッドスポーク組より0.36w空気抵抗が小さいです。
また、スポーク本数32本で比較しますと、CX-RAYは2.0-1.8バテッドスポークより0.47w空気抵抗が小さいです。
後輪ではライダーやフレームが走行風を受ける為、走行風による影響は前輪と比べて小さくなります。
後輪の走行風による影響は前輪のおおよそ3分の1としますと、スポーク本数16本の時でCX-RAYは2.0-1.8バテッドスポークより0.12w空気抵抗が小さいです。
また、スポーク本数32本で比較しますと、CX-RAYは2.0-1.8バテッドスポークより0.15w空気抵抗が小さいです。
この計算結果を下記表にまとめました。
CX-RAYスポークと2.0-1.8バテッドスポークとの空気抵抗の差
| スポーク本数 | 前輪 | 後輪 |
| 16本 | 0.36w | 0.12w |
| 32本 | 0.47w | 0.15w |
この事から、前輪はエアロスポークCX-RAYにする効果が少しありますが、後輪はほとんど効果がありません。
スポーク本数を減らした方が効果的
次は、スポーク本数を減らした時について考察します。
40km/h走行時のスポーク空気抵抗
| スポーク | 前輪 | 後輪 | |
| CX-RAY | 16本 | 1.78w | 0.60w |
| 2.0-1.8バテッド | 16本 | 2.14w | 0.72w |
| CX-RAY | 32本 | 2.29w | 0.77w |
| 2.0-1.8バテッド | 32本 | 2.76w | 0.92w |
前輪の空気抵抗計算値を見てみますと、CX-RAYスポークではスポーク本数16本の方が32本より0.51w空気抵抗が小さいです。
また、2.0-1.8バテッドスポークではスポーク本数16本の方が32本より0.61w空気抵抗が小さいです。
後輪の走行風による影響は前輪のおおよそ3分の1としますと、CX-RAYスポークではスポーク本数16本の方が32本より0.17w空気抵抗が小さいです。
また、2.0-1.8バテッドスポークではスポーク本数16本の方が32本より0.2w空気抵抗が小さいです。
この計算結果を下記表にまとめました。
スポーク本数による空気抵抗の差
| スポーク種類 | 前輪 | 後輪 |
| CX-RAY | 0.5w | 0.17w |
| 2.0-1.8バテッド | 0.61w | 0.21w |
この事から、スポークを変えるよりも、スポーク本数を減らした方が効果が大きい事が分かりました。
おすすめのスポークと本数

手組みフロントホイール
前輪は走行風による影響が大きいですので、スポーク本数を16本にしてCX-RAYスポークを使って手組みしますと、32本のラウンドスポークで手組みしたホイールより1w空気抵抗を減らす事ができます。
CX-RAYはラウンドスポークより価格がかなり高いですが、1本あたり400円で16本使用したとしても6400円ですので、手組み作業の労力を考えますと決して高くありません。
スポーク穴が16個あるハブとリムが用意できれば問題ないですが、入手できない場合はスポーク穴が32個あるハブとリムで代用できます。
スポーク本数32本ラジアル組で組むイメージですが、その内16本のスポークを均一に間引きしますとCX-RAYスポーク16本のフロントホイールが出来上がります。
リムのスポークを通していない穴をテープで塞いでおきますと、雨や塵がリム内に入らなくなります。
ディスクブレーキ用のハブを使う場合は、クロス組にしませんとブレーキを掛けた時にスポークが切れて非常に危険です。
手組みリアホイール
後輪はライダーやフレームが走行風を受ける為、空気抵抗による影響は前輪より小さいです。
また、前輪はリムブレーキモデルの場合では転がっているだけで力の伝達はされていませんが、後輪はペダルを漕いだ力がスポークからリムに伝わりますので、後輪のスポークには剛性が重要になってきます。
CX-RAYは靭性(じんせい)がありますが靭性とは破断のしにくさの事で、靭性が高いと強い力が加わってもスポークがバネの様に伸びますので、スポークが破断しにくいです。
ですが、靭性が高いとペダルを踏み込んだ力の一部がスポークを伸ばす力に奪われてしまいますので、靭性が高すぎると進まないホイールになってしまいます。
高いギヤ比で走る平坦路ではクランク1回転あたりのホイール回転数が多い為、スポークに伝わる力が分散されます。
ですが、低いギヤ比で走る上りではクランク1回転あたりのホイール回転数が少ない為、スポークに伝わる力が集中します。
また、CX-RAYの特徴である空気抵抗の小ささも上りでは速度域が低い為、空気抵抗軽減効果はほとんどありません。
以上の理由により、後輪には伸びにくくて剛性のあるラウンドスポークの使用が適しています。
ラウンドスポークの欠点は空気抵抗が大きいだけではなくスポーク重量が重い事ですが、力の伝達効率を考えますと重量的に不利になったとしても、ラウンドスポークを使用した方がより剛性のあるホイールが組めます。
重量と空気抵抗が気になる場合は、反ドライブ側のみCX-RAYにしますと剛性低下を抑えながら軽量化と若干の空気抵抗が軽減できます。
完組ホイールは軽量高剛性
前輪の場合は駆動剛性が不要ですので、手組みホイールでも使うパーツによっては完組ホイールと同等の物が作れます。
ですが、後輪は駆動剛性が必要ですのでペダルを踏み込む力に負けない剛性のあるパーツ構成にしませんと、ペダルに伝えた力の一部がホイールに吸収されてしまいます。
その為、ホイール組には剛性のあるパーツを選ぶ必要がありますが、そうしますと今度はホイールが重くなりますので、手組みホイールは剛性と軽量化の両立が難しいです。
ですが、完組ホイールはメーカーがハブとスポークとリムを自社設計していますので、剛性と軽量化が両立できています。
剛性が高くて軽いホイールを求めている人は、完組ホイールの購入をおすすめします。
(2024/07/26 19:14:29時点 楽天市場調べ-詳細)
価格も高いですが剛性も高いです。
レーシングゼロと同じ剛性の物を手組みホイールでは同じ重量で作れません。
スポークの空気抵抗を検証

3通りのスポークパターンのホイールを空転させて速度の実測値を取り、得られた実測値を用いて計算をして空気抵抗を数値化しました。
ホイール空転時の失速実測値データ取り
CX-RAYスポーク16本の時と、CX-RAYスポーク32本の時と、CX-RAYスポーク16本と2.0-1.8バテッドスポーク16本をミックスした3通りのスポークパターンで組まれたホイールを用いてテストを実施しました。
ホイールはタイヤやチューブやリムテープを外した状態にして、ホイール以外の影響をなるべく排除しています。
まずは、データ取りするホイールを40km/h以上の速度で空転させます。
そして、40.0km/hまで速度が落ちた所から、次にサイコンに表示される速度を3回分ずつデータ取りしてから平均値を出します。


なお、人手でクランクを回している為、完全に速度を揃える事が困難ですので、実データは±0.1km/hのズレがあります。
CX-RAYスポーク16本
| 1回目 | 2回目 | 3回目 | 平均値 | |
| 計測開始 | 39.9km/h | 40.1km/h | 40.0km/h | 40.0km/h |
| 計測終了 | 38.2km/h | 38.2km/h | 38.2km/h | 38.2km/h |
CX-RAYスポーク32本
| 1回目 | 2回目 | 3回目 | 平均値 | |
| 計測開始 | 40.0km/h | 39.9km/h | 40.1km/h | 40.0km/h |
| 計測終了 | 37.9km/h | 37.8km/h | 38.0km/h | 37.9km/h |
CX-RAYスポーク16本と2.0-1.8バテッドスポーク16本のミックス
| 1回目 | 2回目 | 3回目 | 平均値 | |
| 計測開始 | 40.1km/h | 40.0km/h | 40.1km/h | 40.07km/h |
| 計測終了 | 37.7km/h | 37.7km/h | 37.7km/h | 37.7km/h |
上記表の平均値
| 計測開始 | 計測終了 | 失速値 | |
| CX-RAYスポーク16本 | 40.0km/h | 38.2km/h | 1.8km/h |
| CX-RAYスポーク32本 | 40.0km/h | 37.9km/h | 2.1km/h |
| CX-RAY16本+バテッド16本 | 40.07km/h | 37.7km/h | 2.37km/h |
計測結果を考察しますと、スポーク本数が多いとホイールの回転速度の低下がしやすいです。
また、バテッドスポークよりCX-RAYスポークの方がホイールの回転速度の低下がしづらいです。
実測値からスポークの運動エネルギーを計算
まずは、CX-RAYスポーク16本 計測開始1回目の値39.9 km/hの速度でホイールを回転させた時のスポーク運動エネルギーを計算します。
手順1-1から手順1-8までの計算は下記の値を使用しています。
速度 39.9km/h
スポークの重さ 4.66g
スポークの本数 16本
ニップルの重さ 0.4g
リムの重さ 390g
タイヤ周長 2105mm
※タイヤの周長は時速(km/h)から1分間あたりのホイール回転数(rpm)を計算する為に使用します。
スポークの周速度はハブ軸から離れる程速くなりますので、1cm間隔で細かく計算します。
手順と計算式は下記になります。
手順1-1 速度の単位を時速(km/h)から秒速(m/s)に変換する
\(\frac{速度(km/h)\times1000(mm)}{3600(秒)}\)
\(\frac{39.9\times1000}{3600}\)
=11.083m/s
手順1-2 1分間あたりのホイール回転数(rpm)を計算する
\(\frac{速度(m/s)\times60\times1000}{タイヤ周長(mm)} \)
\(\frac{11.083\times60\times1000}{2105}\)
=315.914rpm
手順1-3 ホイール周上1cmあたりの速度(m/s)を計算する
ホイール周上1cmあたりの速度は4cmから31cmを1cm間隔で28通り計算しますが、まずは半径4cmの時の周速度(m/s)を計算します。
\(\frac{2\times半径(cm)}{100\times円周率π\timesホイール回転数(rpm)\div60}\)
\(\frac{2\times4}{100\times3.14\times315.914\div{1}{60}}\)
=1.323m/s
手順1-4 ホイール周上1cmあたりの運動エネルギーJ(ジュール)を計算する
スポーク総重量は4.66g×16本=74.56gです。
ホイール周上の半径は4cmから31cmを1cm間隔で計算しますが、30cmと31cmはリムとして考えますので、スポークは4cmから29cmまでの 26通り計算します。
スポークは半径1cmあたり\(\frac{74.6g}{26}=2.867g=0.002867kg\)になります。
後は下記計算式に数値を当てはめて計算します。
\(\frac{1}{2}\timesスポーク1cmあたりの重量(kg)\times周速度(m/s)^{2}\)
\(\frac{1}{2}\times0.002867\times1.326^{2}\)
=0.002511J
手順1-5 ホイール周上1cmあたりに掛かる遠心力(×g)を計算する
\(1118\times半径(cm)\timesホイール回転数(rpm)^{2}\times10^{-8}\)
\(1118\times4\times315.914^{2}\times10^{-8}\)
=4.463×g
手順1-6 半径あたりに掛かる圧力(g/cm2)を計算する
\(半径あたりの重量(g)\times遠心力\)
\(2.867\times4.463\)
=12.799g/cm2
手順1-7 「手順1-6 半径あたりに掛かる圧力」と「手順1-2 1分間当たりのホイール回転数」と「手順1-4 ホイール周上1cmあたりの運動エネルギー」の計算結果を用いて運動エネルギー係数を計算する
\(\frac{半径あたりに掛かる圧力(g/cm^{2})}{1分間当たりのホイール回転数}\timesホイール周上1cmあたりの運動エネルギー(J)\times60\)
\(\frac{12.799}{315.914}\times0.002511\times60\)
=0.269
手順1-8 「手順1-2 1分間当たりのホイール回転数」と「手順1-7 運動エネルギー係数」と「手順1-4 ホイール周上1cmあたりの運動エネルギー」の計算結果を用いて、半径あたり回転させるのに必要な運動エネルギー(w)を計算する
\(\frac{1分間あたりのホイール回転数(rpm)}{60}\times係数\times運動エネルギー(J)\)
\(\frac{315.914}{60}\times0.269\times0.002511\)
=0.004w
この要領で半径4cmから31cmまでのホイール回転に必要な運動エネルギーを計算していきます。
半径30cmと31cmは回転させる重量物がリムになりますので、手順1-4の「スポーク」は「リム」に置き換えて計算します。
手順1-9 半径4cmから31cmまで計算した値を合計する
半径4cmから31cmまでの回転に必要な運動エネルギーを手順1-1から手順1-8まで上記計算式で計算した結果、下記表の値になりました。
| 半径(cm) | 運動エネルギー(w) |
| 4 | 0.004 |
| 5 | 0.004 |
| 6 | 0.005 |
| 7 | 0.006 |
| 8 | 0.007 |
| 9 | 0.008 |
| 10 | 0.009 |
| 11 | 0.010 |
| 12 | 0.011 |
| 13 | 0.012 |
| 14 | 0.013 |
| 15 | 0.013 |
| 16 | 0.014 |
| 17 | 0.015 |
| 18 | 0.016 |
| 19 | 0.017 |
| 20 | 0.018 |
| 21 | 0.019 |
| 22 | 0.020 |
| 23 | 0.021 |
| 24 | 0.021 |
| 25 | 0.022 |
| 26 | 0.023 |
| 27 | 0.024 |
| 28 | 0.025 |
| 29 | 0.026 |
| 30 | 1.882 |
| 31 | 1.883 |
計算結果を合計しますとホイールを回転させるのに必要な運動エネルギーが計算できます。
上記表の値を合計した結果、CX-RAYスポーク16本 計測開始1回目39.9 km/hの運動エネルギーは4.128wになりました。
手順1-10 残り17項目のホイール空転時の運動エネルギーを計算して表を完成させる
手順1-1から手順1-9の計算式を用いて、残り17項目の速度データから運動エネルギーを計算します。
複数のスポークの重量から平均重量を計算しますと、CX-RAYスポークは1本あたり4.66gで、2.0-1.8バテッドスポークは1本あたり6.27gです。
CX-RAYスポークと2.0-1.8バテッドスポークの平均重量を計算しますと、
\(\frac{CX-RAY+バテッドスポーク}{2}\)
\(\frac{4.66+6.27}{2}\)
=5.47g
になりました。
ですので、CX-RAYスポークと2.0-1.8バテッドスポークをミックスしたホイールのテストでは、スポーク重量は1本あたり5.47gとして計算しています。
CX-RAYスポーク16本、CX-RAYスポーク32本、CX-RAYスポーク16本と2.0-1.8バテッドスポーク16本のミックスの速度データの合計18項目を計算した所、下記表の値になりました。
CX-RAYスポーク16本
| 1回目 | 2回目 | 3回目 | |
| 計測開始 | 4.128w | 4.169w | 4.148w |
| 計測終了 | 3.783w | 3.783w | 3.783w |
CX-RAYスポーク32本
| 1回目 | 2回目 | 3回目 | |
| 計測開始 | 4.591w | 4.568w | 4.614w |
| 計測終了 | 4.122w | 4.100w | 4.144w |
CX-RAYスポーク16本と2.0-1.8バテッドスポーク16本のミックス
| 1回目 | 2回目 | 3回目 | |
| 計測開始 | 4.748w | 4.725w | 4.748w |
| 計測終了 | 4.197w | 4.197w | 4.197w |
手順1-11 失われる運動エネルギーを計算する
手順1-10の表から平均値を求め、計測開始と計測終了の値の差を計算しますと、下記表の値になりました。
| 計測開始 | 計測終了 | 失われる運動エネルギー | |
| CX-RAYスポーク16本 | 4.148w | 3.783w | 0.365w |
| CX-RAYスポーク32本 | 4.591w | 4.122w | 0.469w |
| CX-RAY+バテッド計32本 | 4.740w | 4.197w | 0.543w |
手順1-12 バテッドスポーク16本と32本の失われる運動エネルギーのデータを手順1-11の表から計算する
バテッドスポークのみでテストデータを取れば確実ですが、手順1-11の表の値からバテッドスポークのみの値を計算する事ができます。
“CX-RAY+バテッド計32本” – “CX-RAYスポーク32本” + “CX-RAYスポーク16本”
0.543-0.496+0.365
=0.439w
\(\frac{CX-RAYスポーク32本}{CX-RAYスポーク16本}\times”2.0-1.8バテッドスポーク16本”\)
\(\frac{0.469}{0.365}\times0.439\)
=0.565w
計算結果を下記表にまとめました。
| 失われる運動エネルギー | |
| CX-RAYスポーク16本 | 0.365w |
| CX-RAYスポーク32本 | 0.469w |
| バテッドスポーク16本 | 0.439w |
| バテッドスポーク32本 | 0.565w |
計算値からスポークの空気抵抗を計算
手順1-12の表の「失われる運動エネルギー」は停車時にホイールを空転させた時の計算値ですが、実走では走行風がホイールにも当たります。
スポークは12時の方向から走行風による影響が小さくなり始め、6時の方向で走行風による影響が一番小さくなります。
そして、6時の方向から走行風による影響が大きくなり始め、12時の方向で走行風による影響が一番大きくなります。
スポークの空気抵抗は速度の3乗に比例しますので、走行風を考慮してスポークの空気抵抗を計算する必要があります。
詳しくは書籍「ロードバイクの科学」の17ページに書かれています。
(2024/07/26 16:56:17時点 楽天市場調べ-詳細)
手順2-1 スポーク1cmあたりの空気抵抗係数を計算する
「ホイール回転数」と手順1-11の表に書かれている「失われる運動エネルギー」と「それぞれの半径」の値を用いて、スポーク1cmあたりの空気抵抗係数を計算します。
今回はハブ軸より半径4cmから29cmまで26通り分をまとめて計算します。
計算は下記の値を使用しています。
手順1-1と手順1-2より
\(\frac{速度(km/h)\times1000(mm)}{3600(秒)}\)
\(\frac{40\times1000}{3600}\)
=11.111m/s
\(\frac{速度(m/s)\times60\times1000}{タイヤ周長(mm)}\)
\(\frac{11.111\times60\times1000}{2105}\)
=316.706rpm
失われる運動エネルギー
手順1-11の表の右上より
0.365w
26通りの半径
4cm 5cm 6cm 7cm 8cm 9cm 10cm 11cm 12cm 13cm 14cm 15cm 16cm 17cm 18cm 19cm 20cm 21cm 22cm 23cm 24cm 25cm 26cm 27cm 28cm 29cm
下記の計算式を用いて計算します。

\(\frac{54\times10^9\times0.365}{3.14^3*316.706^3\times((4^3+5^3+6^3+7^3+8^3+9^3+10^3+11^3+12^3+13^3+14^3+15^3+16^3+17^3+18^3+19^3+20^3+21^3+22^3+23^3+24^3+25^3+26^3+27^3+28^3)+29\times10^5)}\)
=0.000007
手順2-2 スポークの角度をラジアン(rad)に換算する
スポークの角度を本数分だけ分割します。
(16本のスポークを使用した条件で計算していますので16分割しています)
360°を16分割しますと22.5°になります。
走行風は常に水平に当たりますが回転するスポークは風が当たる向きが常に変わりますので、スポークにあたる風速は走行風とスポークの周速度の両方を考慮する必要があります。
スポークが水平に近づく程走行風の影響が小さくなりますので、斜めになった時のスポーク前方投影長さを調べる必要があります。
実際にホイールからスポークの前方投影長さをメジャーや物差しで採寸してもいいですが、計算で求められます。
まずは、スポークの角度をラジアンに換算します。
半円は1ラジアン(rad)3.14(円周率π)ですので、8等分します。
\(\frac{円周率π}{8等分}\)
\(\frac{3.14}{8}\)
=0.392
後は0.392を加算(足し算)し続けていきますと、22.5°間隔のラジアン(rad)が求められます。
手順2-3 前方投影長さの割合を計算する
手順2-2で計算したラジアン(rad)を用いて、三角関数から前方投影長さの割合を計算します。
エクセルや関数電卓を使いますとラジアン(rad)から縦軸長さの割合を割り出せますが、持っていない人は下記の三角関数表の値を使いましょう。
三角関数表(22.5°間隔)
| 角度(°) | ラジアン(rad) | 正弦(sin) | 余弦(cos) | 正接(tan) |
| 0 | 0.000 | 0.000 | 1.000 | 0.000 |
| 22.5 | 0.393 | 0.383 | 0.924 | 0.414 |
| 45 | 0.785 | 0.707 | 0.707 | 1.000 |
| 67.5 | 1.178 | 0.924 | 0.383 | 2.414 |
| 90 | 1.571 | 1.000 | 0.000 | – |
| 112.5 | 1.963 | 0.924 | -0.383 | -2.414 |
| 135 | 2.356 | 0.707 | -0.707 | -1.000 |
| 157.5 | 2.749 | 0.383 | -0.924 | -0.414 |
| 180 | 3.142 | 0.000 | -1.000 | 0.000 |
| 202.5 | 3.534 | -0.383 | -0.924 | 0.414 |
| 225 | 3.927 | -0.707 | -0.707 | 1.000 |
| 247.5 | 4.320 | -0.924 | -0.383 | 2.414 |
| 270 | 4.712 | -1.000 | 0.000 | – |
| 292.5 | 5.105 | -0.924 | 0.383 | -2.414 |
| 315 | 5.498 | -0.707 | 0.707 | -1.000 |
| 337.5 | 5.890 | -0.383 | 0.924 | -0.414 |
| 360 | 6.283 | 0.000 | 1.000 | 0.000 |
Sin(ラジアン(rad))
Sin(0.393)
=0.383
または、上記三角関数表の角度22.5°の正弦(sin)より0.383
手順2-4 スポークにあたる走行風を計算する
手順2-3で計算した前方投影長さの割合に走行風(m/s)を積算(掛け算)しますと、スポークにあたる走行風が計算できます。
40km/h(時速)で走行しますと11.111m/s(秒速)の風がライダーや自転車に当たりますが、スポークはハブ軸を中心に回転しますので、スポークに当たる走行風の風速もスポークの向きによって変わります。
走行風(m/s)×縦軸長さの割合
11.111×0.393
=4.252m/s
手順2-5 半径あたりのスポークの周速度を計算する
回転するホイールはハブから離れる程、周速度が速くなります。
\(\frac{2\times半径(cm)}{100\times円周率π\timesホイール回転数(rpm)\div60}\)
\(\frac{2\times4}{100\times3.14\times316.706\div60}\)
=1.326m/s
手順2-6 スポークに当たる走行風に周速度を加算する
手順2-4で計算したスポークに当たる走行風と手順2-5で計算したスポークの周速度を加算(足し算)します。
スポークに当たる走行風(m/s) + スポークの周速度(m/s)
4.252+1.326
=5.558 m/s
手順2-7 スポークの空気抵抗を計算する
手順2-1で計算した空気抵抗係数と手順2-6で計算したスポークに当たる風速の値を用いてスポークの空気抵抗を計算します。
\(0.5\times空気抵抗係数\timesスポークに当たる風速(m/s) ^3\)
\(0.5\times0.000007\times5.558^3\)
=0.000582w
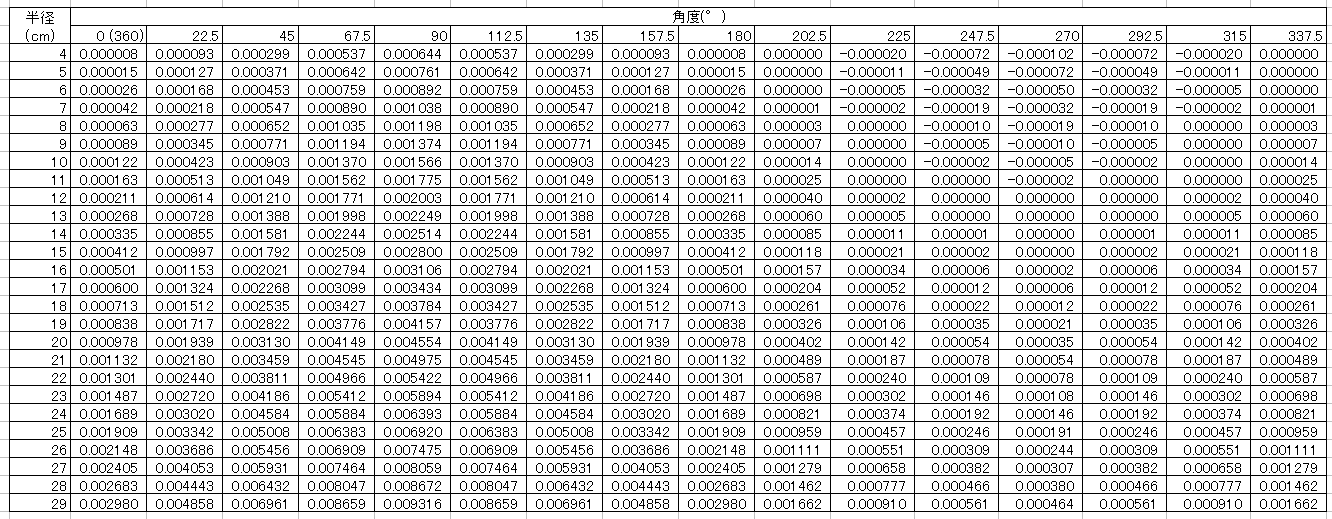
手順2-8 各スポーク角度と各半径の合計416項目の空気抵抗合計値を計算する
手順2-1で求めた空気抵抗係数0.000007を用いて手順2-2から手順2-7の計算を繰り返します。
16通りのスポーク角度
0(360)° 22.5° 45° 67.5° 90° 112.5° 135° 157.5° 180° 202.5° 225° 247.5° 270° 292.5° 315° 337.5°
ホイール中心部からのスポーク半径
4cm 5cm 6cm 7cm 8cm 9cm 10cm 11cm 12cm 13cm 14cm 15cm 16cm 17cm 18cm 19cm 20cm 21cm 22cm 23cm 24cm 25cm 26cm 27cm 28cm 29cm
合計値を計算した所、CX-RAYスポーク16本のスポークで組み立てた前輪を履いて40km/hの速度で走りますとスポーク部で1.782wの空気抵抗が発生する事が計算できました。
後輪のスポークの空気抵抗を計算
後輪はフレームやライダーの後ろに隠れますので、走行風が前輪より当たりにくくなります。
一般的に後輪の空気抵抗は前輪の3分の1ですので、手順2-8で計算した値を3分の1にしますと後輪の空気抵抗値が分かります。
仮に40km/hで走っている時に後輪が受ける走行風を16km/hとして手順2-2から手順2-8で計算した所、0.596wでした。
スポーク空気抵抗の計算結果
40km/h走行時のスポーク空気抵抗
| スポーク | 前輪 | 後輪 | |
| CX-RAY | 16本 | 1.78w | 0.60w |
| 2.0-1.8バテッド | 16本 | 2.14w | 0.72w |
| CX-RAY | 32本 | 2.29w | 0.77w |
| 2.0-1.8バテッド | 32本 | 2.76w | 0.92w |
この記事の冒頭付近にも記載していますが、それぞれの値を計算しますと、前輪はCX-RAYスポークを少ない本数でホイール組する事でスポークの空気抵抗を小さくできます。
ですが、後輪はスポークの種類や本数を変えたとしてもスポークの空気抵抗はほとんど変わりませんので、わずかな空気抵抗軽減にこだわるよりもパワーの伝達効率が高い硬くて剛性のあるホイールにした方が上りでより速く走れます。
まとめ
CX-RAYスポークは空気抵抗軽減に効果があるが、ラウンドスポークでも本数を減らした方がより空気抵抗が軽減できる。
前輪を手組みする場合、スポーク本数を減らしてCX-RAYスポークを使う事でスポークの空気抵抗を軽減できる。
後輪を手組みする場合、スポーク本数を減らしたりエアロスポークを使ったりしても大してスポークの空気抵抗を減らせられず、ライダーの力をより多くリムに伝えられる剛性が強いスポークや本数を多めにしてホイール組した方が上りで力が逃げにくく速く走れる。
完組ホイールはパーツから自社設計しているので、必要な剛性を確保しながら手組みホイールよりも軽い。
スポークを最適化して、空気抵抗軽減と駆動効率向上を両立させましょう。

|
【広告】-ここから- 【広告】-ここまで- |