プロのロードレースでは、ひと昔前より太めのタイヤが主流ですよね。
太いタイヤのメリットが分かる。
細いタイヤでも走行場面によってはメリットがある事が分かる。
転がり抵抗を軽減して速く走りたい人
タイヤの太さと空気圧についてまとめました。
この記事を読んで、転がり抵抗を軽減して速く走りましょう。
それでは、どうぞ。
|
【広告】-ここから- 【広告】-ここまで- |
目次
本記事の要約
タイヤにも体重制限があります。
空気圧を高くしますと、走行中に自転車が跳ねます。
空気圧を低くしますと、パンクしづらくなります。
太いタイヤは細いタイヤより接地面積が大きく、転がり抵抗も増えます。
走行する路面によりタイヤ幅や空気圧の適正値が異なります。
空気圧を落として走ると乗り心地が向上します。
タイヤにも体重制限がある

タイヤは太くなる程ライダーの許容体重が大きくなりますが、タイヤメーカーが推奨している適正空気圧からライダーの体重を算出してみますと、細いタイヤでも太いタイヤでもタイヤメーカーが想定しているライダーの体重はだいたい同じです。
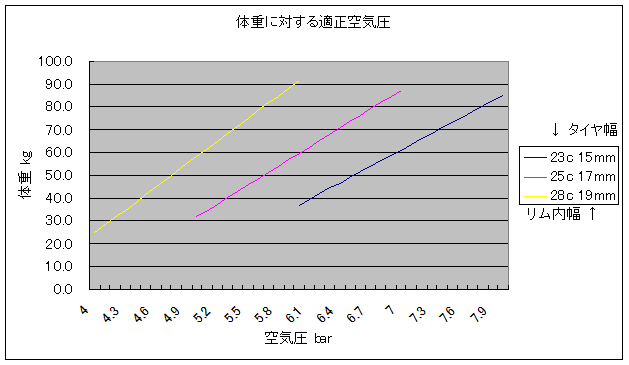
タイヤ適正空気圧算出フォームからタイヤ(コンチネンタル製品)の最大空気圧になる様にライダーの体重を合わせていきますと、以下の表の値になります。
共通条件
自転車重量 10kg
レース用クリンチャータイヤ
| タイヤ幅 | リム内幅 mm | 適正空気圧 bar | 体重 kg |
| 700×23c | 15 | 7.5 | 97.2 |
| 700×25c | 17 | 7.0 | 129.3 |
| 700×28c | 19 | 6.5 | 158.4 |
ですが、メーカーが指定している適正空気圧に合う様に体重の値を調整しますと、以下の表の値になります。
共通条件
自転車重量 10kg
レース用クリンチャータイヤ
| タイヤ幅 | リム内幅 mm | 適正空気圧 bar | 体重 kg |
| 700×23c | 15 | 7.5 | 73.2 |
| 700×25c | 17 | 7.0 | 73.5 |
| 700×28c | 19 | 6.5 | 74.9 |
この事からタイヤの許容体重はタイヤ幅が太くなる程大きくなりますが、メーカーが推奨している適正空気圧でライダーの想定体重を考えますと、ホイールと同様にタイヤにも体重制限があると考えられます。
空気圧が低い程衝撃吸収性が高くなる

柔らかいバネは縮ませやすく反発力が小さいですが、硬いバネは縮ませにくく反発力が強いです。
タイヤも同じで、空気圧を高くする程タイヤが変形しづらく反発力も強くなります。
ですので、路面の凸凹(でこぼこ)でタイヤが変形しづらく反発力が強い為に自転車がタイヤの反発力で跳ねてしまいます。
太いタイヤは細いタイヤよりエアーボリューム量が多く、その分空気圧を落とせます。
路面の凸凹(でこぼこ)でタイヤが柔軟に変形しやすく反発力も弱いですので、路面の状態が悪くても自転車が跳ねにくくスムースに走る事ができます。
タイヤ沈み込み量の計算方法
ライダーの体重を60kg、自転車の重量を10kg、タイヤ空気圧を7kgf/cm2と設定します。
※空気圧の単位kgf/cm2はbarの値と同じです。
分かっている情報はコンチネンタル製品の場合、「タイヤ幅23mm」「タイヤ周長2135mm」「空気圧7kgf/cm2」です。
手順1 タイヤ1本あたりの接地面積を計算
※後輪は前輪より若干荷重が大きく加わりますが、今回は前輪と後輪の荷重を均等になる事とします。
接地面積は体重を空気圧で除算しますと計算できます。
タイヤが2本ありますのでライダーと自転車の合計重量は、タイヤ1本あたりでは合計重量の半分の荷重が加わります。
計算式で表しますと下記になります。
\(接地面積(cm^2)=\frac{ライダーの体重(kg)+自転車の重量(kg)}{2\times空気圧(kgf/cm^2)}\)
\(\frac{60+10}{2\times7}=5cm^2\)
手順2 タイヤ幅の周長を計算
クリンチャータイヤは断面が完全な円ではありませんが、ここでは円として計算します。
円周は直径を円周率で乗算しますと計算できます。
計算式で表しますと下記になります。
\(タイヤ幅周長(mm)=円周率\timesタイヤ幅(mm)\)
\(3.14\times23=72.3mm\)
手順3 タイヤ幅の周長に対するタイヤ周長割合を計算
タイヤ周長割合は「タイヤ周長」を「手順2で求めたタイヤ幅周長」で除算しますと計算できます。
計算式で表しますと下記になります。
\(タイヤ周長割合=\frac{タイヤ周長(mm)}{タイヤ幅周長(mm)}\)
\(\frac{2135}{72.3}=29.547\)
手順4 タイヤ接地幅を計算
「手順1で求めたタイヤ接地面積」と「手順3で求めたタイヤ周長割合」の値を用いて計算します。
計算式で表しますと下記になります。
※1 計算結果をmm単位にしますので、面積cm2で計算した結果に10を乗算しています。
※2 楕円の計算式は縦の半径×横の半径×円周率ですが、半径を直径に表したいですので2で乗算しています。
\(タイヤ接地幅(mm)=\sqrt{\frac{タイヤ接地面積(cm^2)}{タイヤ周長割合\times円周率}}\times10\times2\)
\(\sqrt{\frac{5}{29.547\times3.14}}\times10\times2=4.6mm\)
手順5 タイヤ接地長さを計算
タイヤ接地長さは「手順3で求めたタイヤ周長割合」に「手順4で求めたタイヤ接地幅」を乗算しますと計算できます。
計算式で表しますと下記になります。
\(タイヤ接地長さ(mm)=タイヤ周長割合\timesタイヤ接地幅(mm)\)
\(29.547\times4.6(mm)=137.2mm\)
手順6 ライダーが自転車に乗った時のタイヤ沈み込み量を計算
ここまでの手順を踏まえる事でようやく「タイヤ沈み込み量」が計算する事ができます。
まずはタイヤ半径を計算します。
タイヤ半径はタイヤ周長を円周率で除算しますと計算できます。
計算式で表しますと下記になります。
\(タイヤ半径(mm)=\frac{タイヤ周長(mm)}{円周率}\)
\(\frac{2135}{3.14}=679.6mm\)
上記計算式で求めたタイヤ半径の値を用いて、タイヤ沈み込み量を計算します。
横の値(手順5で求めたタイヤ接地長さ)と斜辺の値(タイヤ半径)は直角三角形で表せられますので、ピタゴラスの定理(三平方の定理)を用いる事ができる為、簡単に計算できます。
※ピタゴラスの定理(三平方の定理)は下記になります。
\(縦^2\times横^2=斜辺^2\)
タイヤ沈み込み量は、タイヤ半径を用いてピタゴラスの定理(三平方の定理)を組み替えて求めた値で減算しますと計算できます。
計算式で表しますと下記になります。
\(タイヤ沈み込み深さ(mm)=\)
\(タイヤ半径(mm)-\sqrt{タイヤ半径(mm)^2-\left(\frac{タイヤ接地長さ(mm)}{2}\right)^2}=\)
\(679.6-\sqrt{679.6^2-\left(\frac{137.2}{2}\right)^2}=3.5mm\)
長くなりましたが、これでタイヤ沈み込み深さを計算できました。
上記計算式を用いて700×25cと28cのタイヤ沈み込み深さを計算した所、下記の値になりました。
| タイヤ | タイヤ周長 mm | 空気圧 kgf/cm2 | 沈み込み深さ mm |
| 700×23 | 2135 | 7.0 | 3.5 |
| 700×25c | 2145 | 6.0 | 3.7 |
| 700×28c | 2155 | 5.0 | 4.0 |
この計算結果から考えますと、タイヤ幅が太い方がより振動吸収性に優れている事が分かります。
適正空気圧にするとパンクしづらくなる

空気圧が高くなる程タイヤが変形しづらくなります。
タイヤのケーシングに柔軟性がありませんと、異物が強くタイヤのケーシングに接触した場合、異物がチューブまで貫通しやすくなりますのでパンクしやすくなります。
空気圧が低いとリム打ちパンクしやすくなりますが、空気圧が高いと異物を踏んだ時にパンクしやすくなりますので、タイヤの空気圧は高すぎず低すぎず適正空気圧にしましょう。
太いタイヤは接地面積が大きい
「ものすごく転がりがいい高級ハブ」のカタログには、タイヤ幅が太い程タイヤの接地している長さが短くなると図解で記載されています。
確かに太いタイヤも細いタイヤも同じ空気圧にした場合、タイヤの接地面積は同じになります。
空気圧を揃えた場合の接地長さ
※タイヤ接地長さは上記計算式手順5で算出できます
| タイヤ幅 mm |
タイヤ周長 mm |
空気圧 kgf/cm2 |
タイヤ接地幅 mm |
タイヤ接地長さ mm |
| 23 | 2135 | 7.0 | 4.6 | 137.2 |
| 25 | 2145 | 7.0 | 5.2 | 131.9 |
| 28 | 2155 | 7.0 | 6.0 | 124.9 |
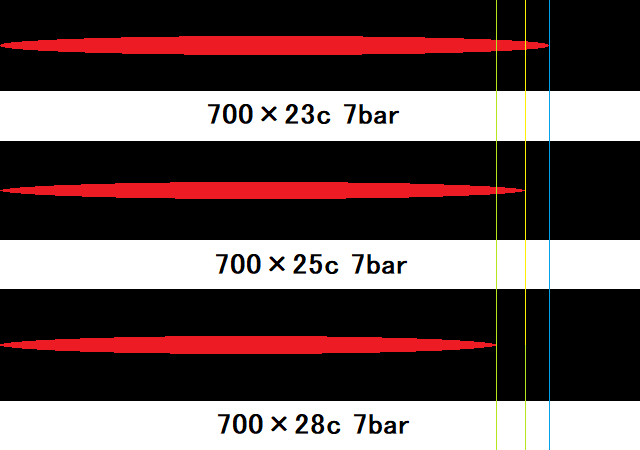
ですが、実際には太いタイヤでは細いタイヤより空気圧を低くしますので、低い空気圧の太いタイヤは高い空気圧の細いタイヤより接地面積が増えます。
空気圧をタイヤ太さに合わせて調整した場合の接地長さ
※タイヤ接地長さは上記計算式手順5で算出できます
| タイヤ幅 mm |
タイヤ周長 mm |
空気圧 kgf/cm2 |
タイヤ接地幅 mm |
タイヤ接地長さ mm |
| 23 | 2135 | 7.0 | 4.6 | 137.2 |
| 25 | 2145 | 6.0 | 4.8 | 142.4 |
| 28 | 2155 | 5.0 | 5.1 | 147.8 |

計算した結果、空気圧をタイヤ太さに合わせて調整した場合、タイヤ接地長さはタイヤ幅が太くなる程長くなる事が計算結果から分かりました。
空気圧が低いと転がり抵抗が大きくなる

タイヤ幅を太くする程エアーボリューム量が増えますので、路面の状態が悪くても走行中に発生する振動を抑制できる為自転車が跳ねにくくなりますが、タイヤの接地面積が広くなる程摩擦抵抗が増えますので自転車が進みにくくなります。
Road Bike Tires Test Resultsの記事には、タイヤの転がり抵抗について取り上げられています。
そのページに記載されている値を抜粋します。
タイヤメーカー:Continental
製品:Grand Prix 5000
タイヤ規格:700×25c
上記タイヤを42.5kgの力で押し当てて28.8km/hの速度で、実験装置で転がした時の転がり抵抗は以下の値です。
8.3bar の時 転がり抵抗10.0ワット
6.9bar の時 転がり抵抗10.7ワット
この事から空気圧が低くなる程、転がり抵抗が増える事が分かります。
路面や速度に合ったタイヤ幅や空気圧にする

実験装置ではローラーの表面に凸凹(でこぼこ)がないかもしれませんが、実走では路面の状態が常に変わります。
舗装したばかりの状態の良い路面もあれば、経年劣化でガタガタになっている路面もあります。
また、走行速度が速くなる程、タイヤ接地面から発生する振動が大きくなります。
振動で自転車が跳ねる事による抵抗とタイヤの転がり抵抗のバランスを考えて、路面に合ったタイヤの幅と空気圧を決めます。
平坦路走行で路面の状態が良い場合は細めのタイヤ700×23cがおすすめです。
平坦路走行で路面の状態が悪い場合は太めのタイヤ700×28cがおすすめです。
ヒルクライムをする場合は路面が悪くても速度域が低い為、細めのタイヤ700×23cがおすすめです。
あらゆる路面や速度域でも万能に使いたい場合は、中間幅のタイヤ700×25cにしますと無難です。
使用するタイヤの太さを決めましたら、後は空気圧を路面に合わせて調整しますと最も路面に適した抵抗が小さい良く進む自転車にできます。
(2024/07/27 11:48:27時点 楽天市場調べ-詳細)
(2024/07/27 14:52:47時点 楽天市場調べ-詳細)
(2024/07/27 00:10:05時点 楽天市場調べ-詳細)
空気圧を変えて走行時間を比較した結果

今までは後輪のタイヤ700×23cの空気圧を8barと高めにしていましたが、7barに落として同じ平坦路コースを走りました。
同じ平均パワーの走行ログで比較しましたが、風向きが違ったり路面の状態が変わっていたりしているかもしれませんし、信号の停止時間も違いますのでデータは参考程度に見て下さい。
空気圧8barの時、走行時間2時間52分16秒
空気圧7barの時、走行時間2時間51分45秒
空気圧を変えても走行時間に差はほぼありませんでした。
ですが、自転車から伝わる振動は空気圧が高い時はかなり強かったですが、空気圧を適正圧まで下げた所、空気圧が高い時より自転車に加わる振動はかなり減退されました。
まとめ
タイヤメーカーが推奨している適正空気圧からライダーの体重を算出した場合、細いタイヤでも太いタイヤでも想定しているライダーの体重はだいたい同じである。
空気圧を高くする程タイヤが変形しづらく反発力も強くなるので、路面の状態が悪いと自転車がタイヤの反発力で跳ねてしまう。
空気圧が低いとタイヤの柔軟性が増すので、異物を踏んでもパンクしづらくなる。
太いタイヤは適正空気圧が低いので、細いタイヤより接地面積が大きい。
空気圧が低いと接地面積が増える事で、転がり抵抗が大きくなる。
タイヤ幅や空気圧の設定には一長一短があるので、路面や走行場面に合った物にする。
空気圧を落として走ると乗り心地が向上する。
タイヤ幅と空気圧を最適化して、速く快適に走りましょう。



|
【広告】-ここから- 【広告】-ここまで- |








